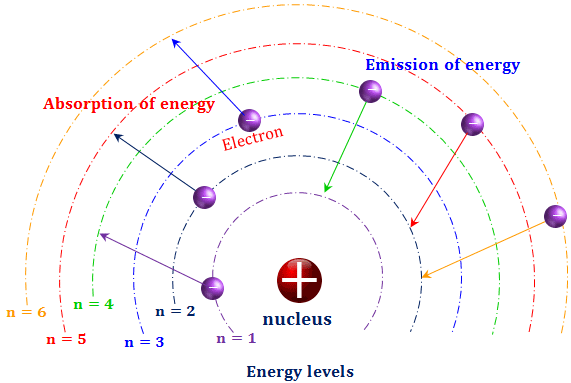
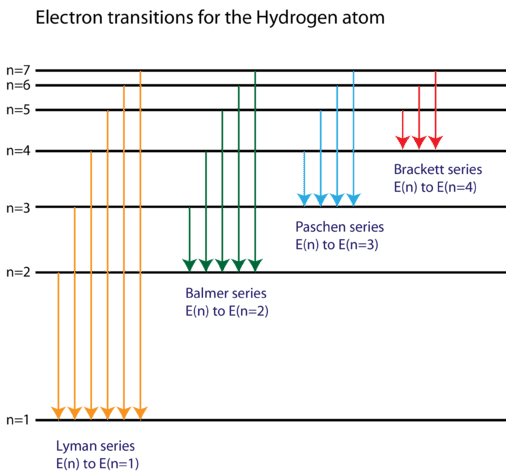
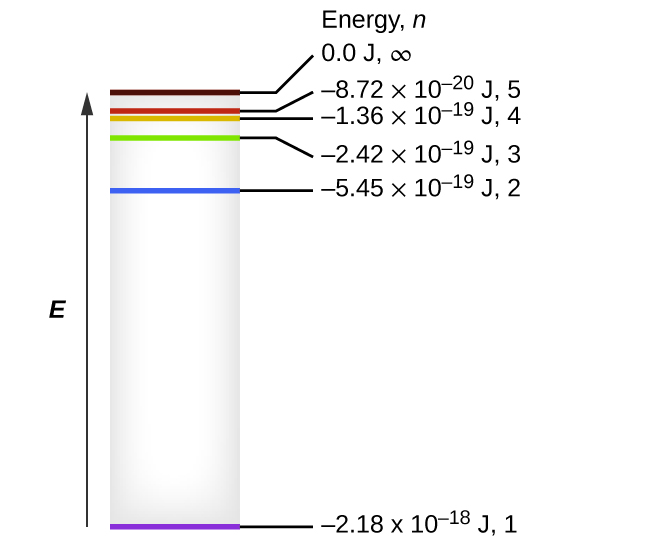
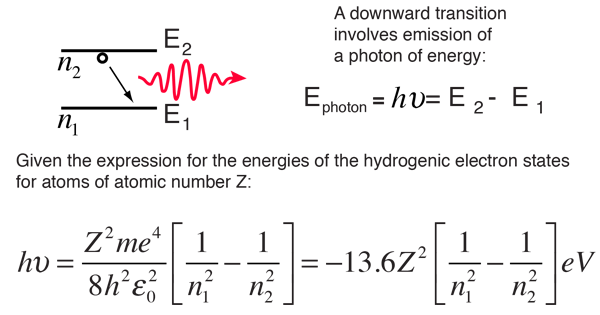
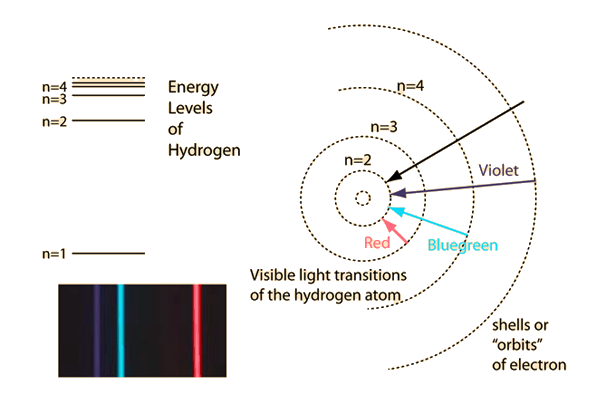
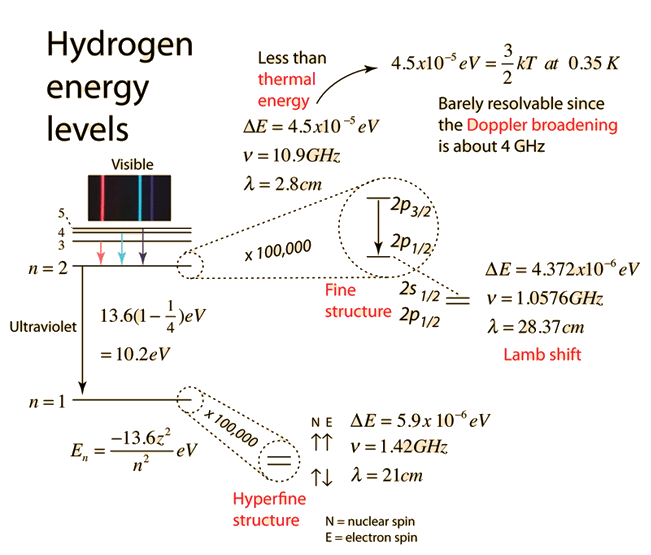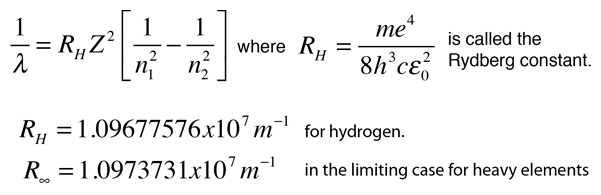What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the
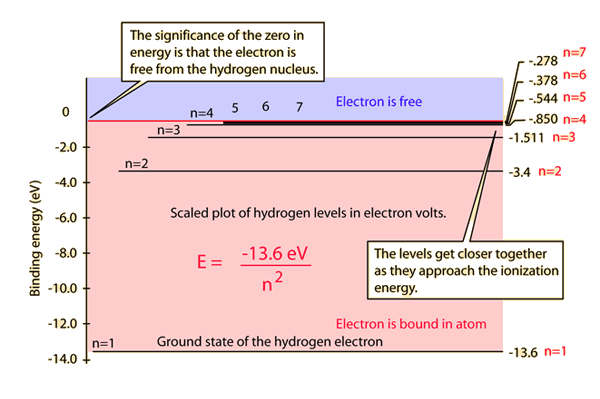
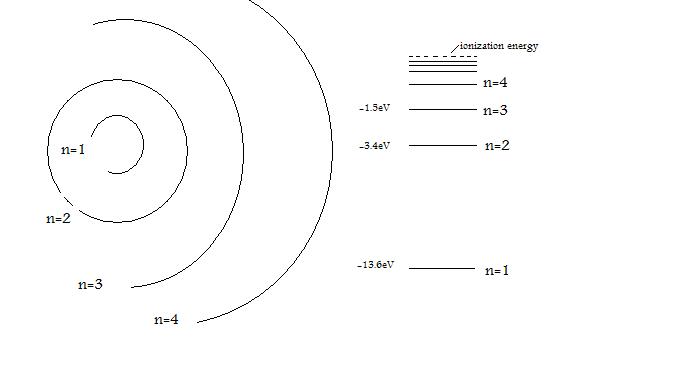
The energy of the electron in the ground state of hydrogen atom is - 13.6 eV. Find the kinetic energy and potential energy of electron in this state.
The electron energy in hydrogen atom is given by En=(−2.18×10^
The electron energy in hydrogen atom is given by En = -217 x 10^-12/n^2 ergs. - Sarthaks eConnect | Largest Online Education Community
Energy Levels in Atoms
Bohr Model Hydrogen Atom - Postulates, Energy Levels
5.7: Spectral Lines of Atomic Hydrogen - Chemistry LibreTexts
Hydrogen energies and spectrum
6.2 The Bohr Model – Chemistry
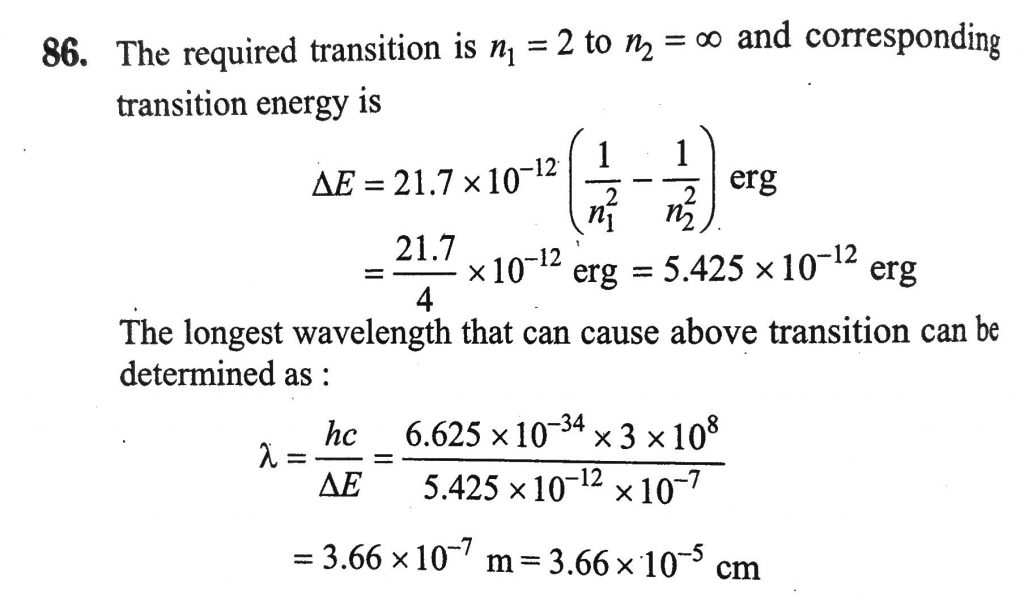
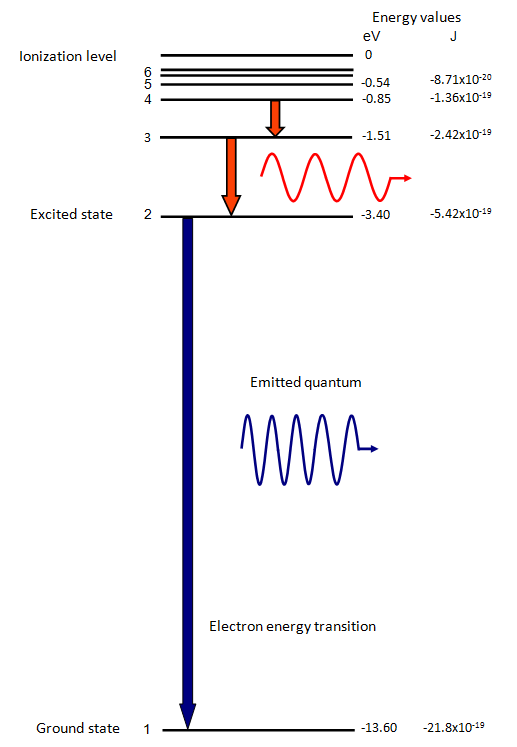
The electron energy in hydrogen atom is given by En =(−21.7×10^−12 )n^2 erg. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest
Hydrogen energies and spectrum
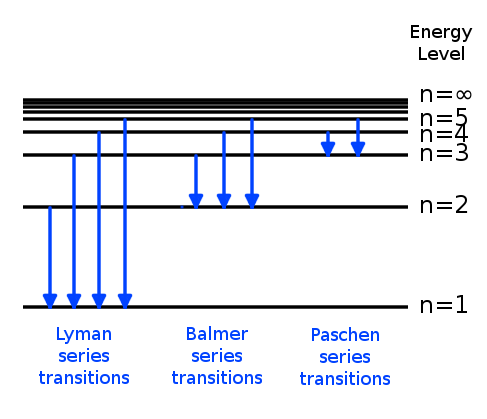
How can an electron leap between atomic levels without passing through all the space in between? | Science Questions with Surprising Answers
schoolphysics ::Welcome::
Solved QUESTION 2: ENERGY LEVELS OF THE HYDROGEN ATOM The | Chegg.com
Bohr's Hydrogen Atom - Chemistry LibreTexts
The ionization cross section of a hydrogen atom vs. electron energy x =... | Download Scientific Diagram
The electron energy in hydrogen atom is given by En = (-2.18 x 10-18)/n2 J. Calculate the energy required to remove an electron completely from the n=2 orbit. What is the longest
Hydrogen energies and spectrum
In the lowest energy level of hydrogen atom, the electron has the angular momentum - YouTube
The electron energy in hydrogen atom is given by .12 21.7x10 ? | Scholr™
The electron energy of hydrogen atom in the ground state works out to be - 2.18 xx 10^(-18) J per atom. Calcu
Hydrogen energies and spectrum
The electron energy in hydrogen atom is given by En = ( - 2.18 × 10^-18) n^2 joules.Calculate the energy required to remove an electron completely from the n = 2 orbit.
